Modéliser une épidémie pour comprendre l’effet des mesures sanitaires collectives prises durant l’épidémie de la Covid 19
Utiliser un modèle d’une épidémie pour tester l’impact de différentes stratégies collectives telles que le port du masque, le confinement de la population et la vaccination de la population sur l’épidémie de la COVID-19.
Place de la séance dans la séquence
Niveau Seconde - Fin du thème 3 : Microorganismes et santé / Agents pathogènes et maladies vectorielles
On cherche à utiliser un modèle d’une épidémie pour tester l’impact de différentes stratégies collectives telles que le port du masque, le confinement de la population et la vaccination de la population.
Objectifs
– Compétences travaillées : modéliser, importance de la modélisation témoin pour déduire l’impact d’une mesure sanitaire
– Savoir établi : Les comportements individuels et collectifs permettent de limiter la propagation (gestes de protection, mesures d’hygiène, vaccination, etc.)
Outil(s) numérique(s) utilisé(s) :
– Création d’une page internet pour les consignes et documents ressources (PAGE de l’ENT)
– Utilisation de Edu’Modèles :
https://www.pedagogie.ac-nice.fr/svt/productions/edumodeles/algo/index.htm
L’outil est assez simple d’utilisation avec une prise en main relativement intuitive. Il s’agit de définir les différents agents c’est-à-dire des acteurs impliqués dans le modèle ainsi que des règles, c’est-à-dire les réactions qui interagissent entre les agents. Dans un modèle épidémique, les agents seront à minima les agents sains, les agents malades et les agents immunisés, les agents morts éventuellement (c’est le cas choisi ici). On peut choisir pour chaque agent, leur nombre ainsi que leur probabilité de déplacement.
Les règles sont au nombre de 3 :
- la règle de contamination qui détermine le comportement entre un agent malade et un agent sain dont la rencontre formera 2 agents malades selon une certaine probabilité, que l’on peut choisir (25% choisi ici),
- la règle de guérison déterminant le comportement d’un individu malade qui pourra guérir, passé un certain délai que l’on choisit, selon une certaine probabilité, choisie également,
- la règle de mortalité déterminant le comportement d’un individu malade qui pourra mourir, passé un certain délai que l’on choisit, selon une certaine probabilité choisie très faible ici.
Il faut penser à décocher la case présente en bas des boite de dialogue « règle » car le choix des « réactifs » » n’ont aucun impact.
Il est également préférable de limiter la durée de la simulation (300 tours choisis ici) pour conserver les données pertinentes situées en début de simulation.
Le curseur de l’ « échelle horizontale » peut être déplacé vers la droite au maximum ainsi que le graphique étiré pour une meilleure visibilité.
Il suffit ensuite de lancer la simulation. Attention, plusieurs simulations donneront des résultats légèrement différents puisque les déplacements des agents sont aléatoires : une certaine variation peut donc être observée dans les résultats finaux de différentes simulations.
Le modèle établi peut être enregistré (icône « enregistrer ce modèle » avec un enregistrement par défaut dans l’espace « téléchargement » de l’ordinateur.
Il est également possible d’ « exporter le graphique » sous format .csv.
On peut par la suite « charger un modèle » déjà établi.
Le modèle témoin peut être soit élaboré avec les élèves à partir d’un modèle vierge, ou mis directement à leur disposition et commenté.
Déroulement de la séance de TP (1h30) :
– Modalité : En présentiel et/ou en visioconférence synchrone ou asynchrone pour des élèves en distanciel
– Outils numériques : PAGE de l’ENT pour les documents et consignes + Webconférence de l’ENT + modèle épidémique témoin fourni
Fichier du modèle à enregistrer et à ouvrir avec Edu’modèles : « charger un modèle »
– Organisation de la séance de travail :
1) Présentation du modèle témoin par le professeur et des différents paramètres impliqués (déplacement, % réaction,…) dans Edu’Modele (élaboration en commun ou mise à disposition dans un dossier partagé.
2) Distribution du travail au sein de la classe : Chaque élève (ou binôme) choisit de tester une des mesures sanitaires : masque ou confinement ou vaccination.
3) Laisser les élèves réfléchir à la modification du paramètre à changer pour modéliser au mieux la mesure :
- Taux de déplacement pour le confinement (pas de valeur exacte attendue)
- Taux de contamination pour le port du masque (pas de valeur exacte attendue)
- Taux d’individus vaccinés dans la population (pas de valeur exacte attendue)
4) Regrouper les élèves/binômes ayant étudié les mêmes mesures pour comparer leurs résultats
5) Présentation orale par un rapporteur du groupe de l’effet de la mesure étudiée sur l’épidémie (les autres complètent la fiche réponse)
6) Évaluation de la robustesse du modèle par la confrontation des données obtenues par la modélisation avec les données épidémiologiques réelles : on peut établir la fiabilité d’un modèle en confrontant les données prédites par le modèle et les paramètres mesurés dans la réalité : plus un modèle est proche des courbes épidémiques mesurées dans la population, plus le modèle correspond à la réalité et donc plus il est fiable.
7) Expliquer brièvement les différentes causes impliquées dans l’évolution en plusieurs vagues dans l’épidémie de la Covid-19
Consignes et documents fournis aux élèves :
Nous vivons actuellement une épidémie mondiale liée à un nouveau virus : le SARS-Cov2. Différentes mesures sanitaires ont été prises pour gérer au mieux la crise sanitaire : les gestes barrières, les confinements et la vaccination de la population.
On cherche à comprendre l’intérêt de ces différentes mesures et leur impact sur l’évolution de l’épidémie.
DOCUMENT RESSOURCES
Document 1 : La notion de modèle mathématique
Parfois, pour étudier un phénomène complexe, comme une épidémie, on peut faire appel à la création de modèle mathématique. Un modèle mathématique est un type de modèle scientifique qui emploie un formalisme mathématique pour exprimer des relations, des prédictions, des variables, des paramètres, des entités et des relations entre des variables et/ou des entités ou opérations. Ces modèles servent à analyser les comportements de systèmes complexes dans des situations difficiles à observer dans la réalité. L’établissement de modèle permet de tester l’impact d’un paramètre sur le phénomène complexe.
Il convient dès à présent de préciser que les modèles mathématiques sont des modèles simplifiés, ayant des limites dont il faut être conscient. Ils restent toutefois utiles pour tenter de prévoir l’évolution d’une épidémie.
Les scientifiques ont modélisé l’évolution d’une épidémie virale dans un modèle nommé SIR selon les règles suivantes :
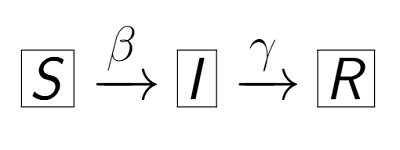
- Règle de contamination selon le taux de transmission β, c’est à dire le taux de personnes saines qui deviennent infectées
- Règle de guérison selon le taux de guérison γ, c’est à dire le taux de personnes infectées qui deviennent retirées (ou immunisées)
Document 2 : Données épidémiologiques de l’épidémie à la COVID-19 de février 2020 au printemps 2021
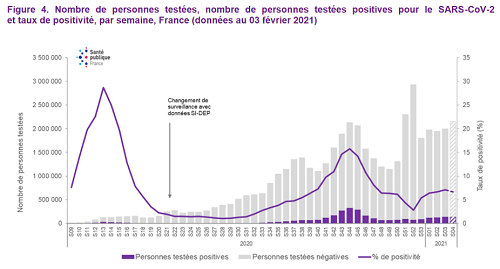
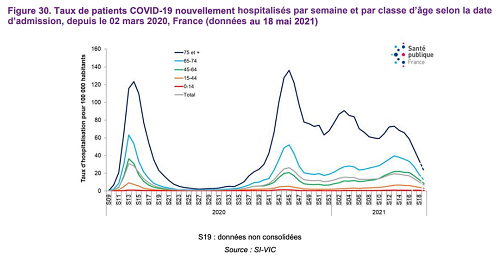
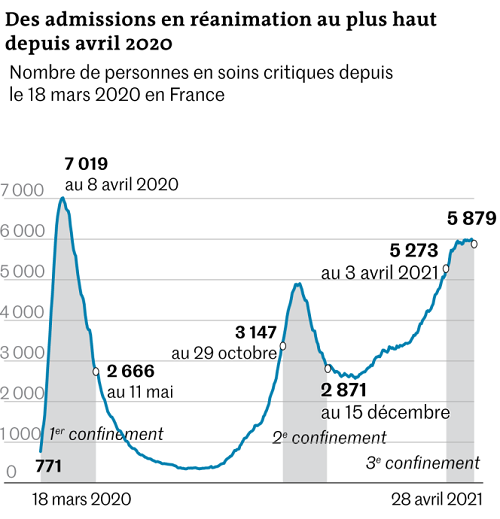
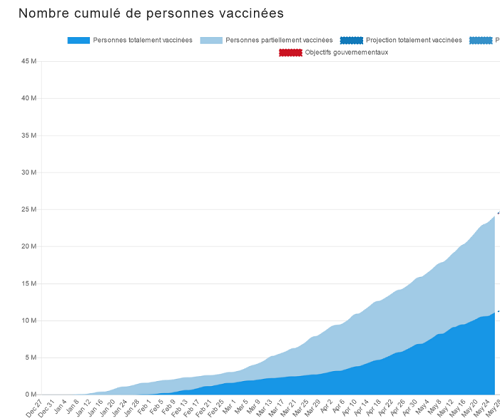
(d’après Santé Publique France, CovidTracker, Geodes)
ACTIVITÉ
Un modèle SIR est à votre disposition : fichier modèle épidémie témoin (à ouvrir avec Edu’modèles/charger un modèle)
| Environnement : 100 lignes et 100 colonnes - Durée : 300 tours | ||||
| Agents | Individu sain Carré plein bleu Probabilité de déplacement : 80% Effectif initial : 800 |
Règles | Contamination type : réaction entre agents Probabilité : 25% Réactifs : individu sain, individu malade Produits : individu malade, individu malade | |
| Individu malade Carré plein orange Probabilité de déplacement : 80% Effectif initial : 40 |
Guérison type : réaction entre agents Probabilité : 50% Age minimal des réactifs : 50 tours Réactifs : individu malade Produits : individu immunisé | |||
| Individu immunisé Carré plein vert Probabilité de déplacement : 80% Effectif initial : 0 |
Mortalité type : réaction entre agents Probabilité : 2% Age minimal des réactifs : 50 tours Réactifs : individu malade Produits : individu mort | |||
| Individu mort Carré plein jaune Probabilité de déplacement : 0% Effectif initial : 0 |
||||
1) Établir les caractéristiques d’une épidémie virale témoin
a. Vous pouvez alors lancer l’animation et visualiser le graphique qui s’affiche montrant l’évolution de chaque agent (en ayant mis le curseur de l’échelle horizontale le plus à droite possible).
b. Compléter le tableau réponse en complétant les paramètres initiaux puis avec les indicateurs clés d’une épidémie virale.
2) Modifier le modèle initial d’une épidémie virale pour modéliser une des stratégies de lutte collective et en déduire leur effet sur l’épidémie
a. Modifier les paramètres du modèle pour simuler les différentes mesures :
- Port du masque
- Confinement
- Vaccination de la population (par la création d’un nouvel agent)
b. Compléter le tableau réponse avec les indicateurs épidémiques correspondants et représenter sur le graphique le pic épidémique pour chaque stratégie collective. En déduire l’impact (et donc l’intérêt) de chaque stratégie sur l’évolution épidémique.
c. Confronter vos résultats aux autres élèves ayant simulé le même paramètre que vous. Discuter des différents résultats obtenus.
d. Présenter oralement vos résultats (un élève rapporteur par groupe) : des données chiffrées doivent appuyer votre raisonnement.
e. Compléter votre fiche réponse d’après les résultats présentés oralement par les autres groupes sur les autres mesures sanitaires.
3) Discuter de la pertinence du modèle obtenu en confrontant les données du modèle aux données épidémiologiques réelles
4) Expliquer brièvement les différentes causes impliquées dans l’évolution en plusieurs vagues dans l’épidémie de la Covid-19.
FICHE RÉPONSE ÉLÈVE :
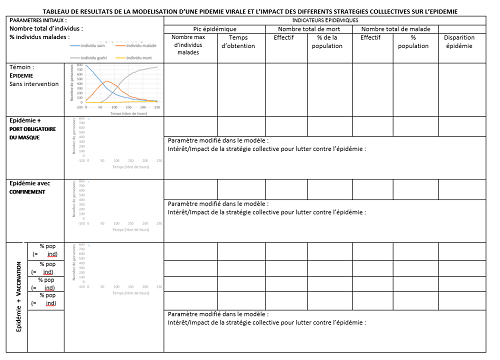
ÉLÉMENTS ATTENDUS
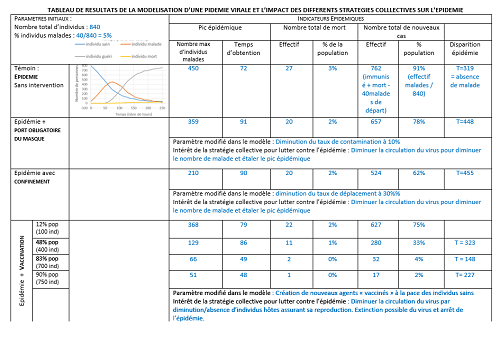
Attention : chaque simulation donne des résultats différents !
Le port du masque : permet de réduire le taux de contamination (91% → 78%) mais n’agit pas significativement sur la mortalité (3% → 2%). On remarque aussi un retardement (72 → 91) et une atténuation (450 → 359) du pic épidémique. C’est une mesure efficace pour diminuer la pression sur les urgences.
Le confinement : permet de réduire considérablement le taux de contamination (91% → 62%) mais également sur le nombre de mort (3% → 2%). On observe un retardement du pic épidémique (72 → 90) mais beaucoup plus atténué (450 → 210). Cette mesure est très efficace si les malades sont isolés chez eux. C’est une mesure efficace pour diminuer la pression sur les urgences.
La vaccination : permet de réduire plus au moins la contamination (91% → 77% ;33% ;4% ;2%) en fonction de la couverture vaccinale (du pourcentage d’individus vaccinés dans la population ) et peut rendre le taux de mortalité nul.
Plus la couverture vaccinale est grande et plus on se rapproche de l’immunité collective. En ce qui concerne le pic épidémique, il arrive plus rapidement (76 → 76 ;57 ;47 ;45) et tend logiquement à devenir de plus en plus faible (500 → 357 ;185 ;76 ;46).
La vaccination est efficace individuellement puisque les personnes vaccinées sont protégées. Mais la mesure n’a une efficacité collective que si la couverture vaccinale est suffisamment grande. (voir Séance Modélisation de la stratégie vaccinale)
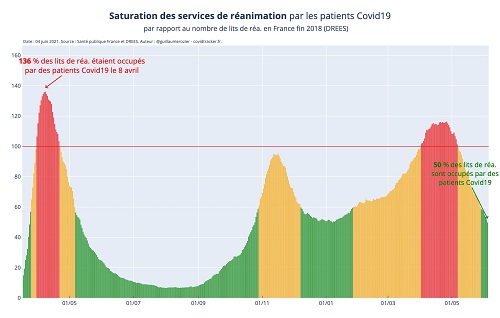
D’après CovidTracker
En confrontant les résultats des modélisations avec les données épidémiologiques, on voit que chaque pic épidémique prend fin après décision de mesures de confinement. La modélisation montre que le confinement tend à diminuer l’amplitude des pics épidémiques. Donc la modélisation semble pertinente pour décrire l’évolution de l’épidémie.
La modélisation de l’impact du port du masque montre aussi un pic épidémique plus aplati, avec une pente plus faible. C’est également ce que l’on observe depuis l’été 2020, où le port du masque a été rendu obligatoire, les pentes des 2 pic épidémiques sont plus faibles qu’au printemps 2020.
Le modèle permet donc d’expliquer les données du réel. Le modèle est donc robuste et fiable.
Bilan :
Le 1er pic épidémique (en mars 2020) a été freiné par les mesures de confinement, ce qui a provoqué la forte diminution des contaminations et donc diminuer le nombre de malades.
La levée des restrictions sanitaires en été puis automne 2020 a permis au virus de circuler davantage (augmentation du taux de contamination et donc du nombre de malades), aboutissant à un 2ème pic épidémique (max atteint en novembre 2020). Ce pic présente cependant une pente plus faible que lors de la 1ère vague, pouvant s’expliquer par le port du masque et le respect des gestes barrières.
Le pic est freiné par le 2ème confinement qui limite les déplacements des personnes et donc diminue le taux de contamination.
Le 3ème pic épidémique est freiné par de nouvelles restrictions de circulation.
La vaccination a débuté en France mais au 28 avril, seul 6 M personnes sont totalement vaccinés c’est-à-dire à peine 10% de la population française (20M ayant eu 1 ou 2 doses, soit 30% de la population). Ce taux de vaccination permet une protection individuelle mais n’assure pas encore une protection collective de la population (notion d’immunité collective).







