Sciences de la vie et de la Terre

Vous trouverez ci-dessous une proposition d’activité d’une heure pour modéliser l’expérience de Luria-Delbrück. Cette expérience a permis de déterminer que les mutations à l’œuvre dans le processus de l’évolution sont dus au hasard et ne sont pas induites par l’environnement.

Cette activité a été créé à partir du travail de La main à la pâte. L’association propose déjà une modélisation à l’aide d’un jeu de cartes et d’un dé. J’ai voulu proposer une version numérique de la modélisation.

I. À propos du logiciel

SCRATCH est un logiciel de programmation avec une interface graphique agréable et intuitive. Il suffit d’agencer des blocs de manière logique pour réaliser un algorithme ou une application simple.

II. Quels étaient les objectifs ?

Cette séance de programmation avec SCRATCH est l’occasion de faire travailler les élèves sur les points suivants :

Domaine du socle et éléments signifiants
Domaine 1 - Composante 3 : Comprendre, s’exprimer en utilisant les langages mathématiques, scientifiques et informatiques. Utiliser l’algorithmique et la programmation pour créer des applications simples.

Programme
Thème 2 : Mettre en évidence des faits d’évolution des espèces et donner des arguments en faveur de quelques mécanismes de l’évolution : maintien des formes aptes à se reproduire, hasard, sélection naturelle.

Cadre de référence des compétences numériques
I.3.4 Écrire des programmes et des algorithmes pour répondre à un besoin (automatiser une tâche répétitive, accomplir des tâches complexes ou chronophages, résoudre un problème logique…) et pour développer un contenu riche (jeu, site web…) (avec des environnements de développement informatique simples, des logiciels de planification de tâches…).

III. Quel a été le déroulement de la séance ?

Pré-requis
Lors des séances précédentes, les élèves ont découvert la théorie de l’évolution. Ils ont pu voir qu’au cours des générations, les descendants diffèrent légèrement de leurs parents suite à l’apparition de variations dans leurs caractères, causées par des mutations. Si ce processus se répète pendant de nombreuses générations, il est possible que les descendants soient très différents de leurs ancêtres. Ils ont également pu aborder des exemples de sélection naturelle.

Phase de motivation (10 minutes)
Je projette la vidéo suivante pour énoncer le problème :

Cette vidéo fait parler Geoffroy de Saint Hilaire, partisan du transformisme au XIXème siècle. Saint Hilaire est d’accord avec l’idée d’un changement de forme au cours du temps mais il pense que les changements sont induits par l’environnement (le concept de mutation n’étant pas encore connu à l’époque).

A la suite de cette vidéo, je demande à chaque élève de se situer sur une échelle de confiance envers le transformisme.

La très grande majorité des élèves ont une confiance forte dans l’hypothèse de Saint-Hilaire.

Pour mettre à l’épreuve leur degré de confiance, je propose aux élèves l’explication de Alfred Russel Wallace. Tout comme son contemporain Charles Darwin, Alfred Russel Wallace a proposé que les variations de la descendance se font de manière aléatoire (même s’il n’était pas en mesure de parler de mutation puisque le concept de gène n’était pas alors connue). J’ai volontairement choisi de citer A. Wallace plutôt que C. Darwin pour que les élèves se basent sur les idées et non sur la renommée des chercheurs.

Le problème suivant est donc mis en place : Comment expliquer l’origine des mutations qui ont pour conséquences des "changements de forme" des êtres vivants au cours du temps (de génération en génération) ?

On se retrouve donc avec deux hypothèses :
– selon Saint-Hilaire, les mutations seraient provoqués par le changement de l’environnement ;
– selon Wallace, les mutations se feraient au hasard et en permanence. L’environnement sélectionne alors les individus porteurs de certaines mutations.

Je leur propose d’éprouver les deux hypothèses, celle de Saint-Hilaire et celle de Wallace, grâce à une modélisation numérique se basant sur le prix Nobel de 1969 obtenu par S. Luria et M. Delbrück.

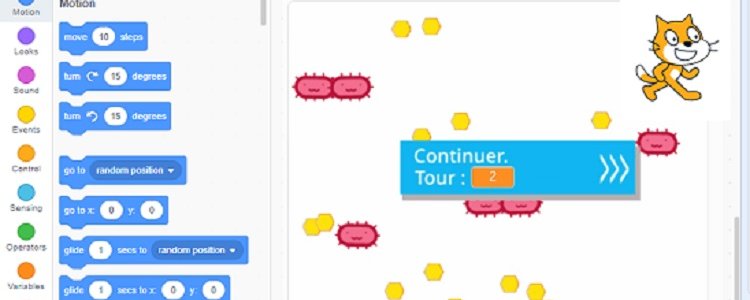
Dans cette modélisation, des bactéries se déplaceront dans un environnement ayant des ressources limitées durant un tour de jeu d’une durée de 6 secondes. A l’issue de ce laps de temps, les bactéries n’ayant prélevé aucun nutriment meurent, celles qui ont prélevé un nutriment survivent, celles qui en ont prélevé au moins deux survivent et se reproduisent. Au bout de 5 tours, des virus spécifiques de ces bactéries (bactériophages) se propagent dans l’environnement et provoquent la lyse des bactéries sensibles en cas de contact. Selon les contacts, cette situation peut durer de 2 à 4 tours. Enfin, la modélisation doit permettre aux bactéries de muter : elles pourront soient muter aléatoirement à n’importe quel moment (hypothèse de Wallace) soit muter aléatoirement uniquement en présence des virus (hypothèse de Saint-Hilaire).

Je montre aux élèves la modélisation réalisée avec scratch et j’explique qu’il est incomplet : il y a seulement des bactéries immobiles et des nutriments dans un environnement. Tout le reste devra être programmé.

La consigne suivante est donnée aux élèves : Complétez le programme informatique pour tester les hypothèses de Saint-Hilaire et de Wallace. Vous pourrez ensuite déterminer la modélisation qui se rapproche le plus de la réalité par comparaison avec des résultats obtenus sur des vraies bactéries. Ces résultats sont disponibles sur le site de La Main à la Pâte, dans la fiche activité disponible en bas de page ou tout simplement dans le prochain paragraphe.

Phase d’activité (40 minutes)
En salle informatique, les élèves ouvrent le fichier pdf tutoriel sur leur ordinateur (lien disponible en bas de page).
Un lien dans le fichier pdf les redirige vers le programme scratch à compléter. En suivant étape par étape le tutoriel, les élèves vont compléter la modélisation. Les étapes sont de plus en plus complexes. Lors de la première étape, les élèves doivent recopier un script pour permettre le déplacement des bactéries. Lors de la seconde étape, il doivent sélectionner et recopier parmi 4 scripts celui qui permettra aux bactéries de se nourrir et de produire de l’énergie. Ensuite, les élèves doivent créer un script à partir d’une sélection de blocs pour que les bactéries meurent au contact d’un virus (sauf si elles ont muté). Enfin, lors de la dernière étape, les élèves doivent compléter un script pour que les mutations soient aléatoires ou induites par l’environnement.

Une fois le modèle terminé, l’élève lance la simulation.

• une simulation avec des mutations au hasard ;
• une simulation avec des mutations uniquement en présence des virus.

A chaque simulation, l’élève doit remplir un tableau. Il indique ainsi le nombre de bactéries survivantes à la fin du dernier tour de la simulation. Il relance 3 fois chaque simulation puis partage ses résultats avec deux autres élèves. Ceux qui n’ont pas fini peuvent récupérer les résultats des autres.

Voici ce qu’il est possible d’obtenir :

• Simulation en testant l’hypothèse de WALLACE : 0, 0, 4, 6, 0, 1, 4, 0, 3
• Simulation en testant l’hypothèse de SAINT-HILAIRE : 1, 0, 0, 2, 0, 0, 0, 2, 0
• Test in situ sur de (vraies) bactéries : 1, 4, 0, 0, 12, 0, 9, 0, 0

L’analyse des résultats laisse à penser que la simulation selon Wallace est plus proche de la réalité que celle de Saint-Hilaire. En effet, la dispersion des valeurs selon Wallace est plus proche de la réalité que celle de Saint-Hilaire. Cette dispersion peut se mesurer en calculant la variance des séries de données. Pour simplifier la notion de dispersion et de variance, les valeurs obtenues dans chaque situation se répartissent sur une plage plus ou moins grande (de 0 à 6 selon la simulation en testant l’hypothèse de Wallace contre seulement de 0 à 2 pour la simulation de l’hypothèse de Saint-Hilaire). Comme la variance n’est pas une notion du cycle 4, j’effectue le calcul au tableau avec un tableur pour leur donner. Voici la moyenne et la variance avec les données obtenues précédemment :

• simulation selon WALLACE : moyenne de 2 et variance de 4,67 ;
• simulation selon SAINT-HILAIRE : moyenne de 0,56 et variance de 0,69 ;
• réalité sur des bactéries : moyenne de 2,89 et variance de 18,54.

Les élèves doivent alors conclure et rédiger une phrase du style : "Les résultats corroborent l’hypothèse..."

Bilan de la séance (5 minutes)
En fin de séance, je lis les différentes conclusions des élèves pour m’assurer qu’ils ont bien réfuté l’explication de Saint-Hilaire et corroboré l’explication de Wallace.

Nous prenons le temps de rédiger le bilan de l’activité.
« Les mutations à l’origine des variations de génération en génération se font au hasard et indépendamment de l’environnement. Autrement dit, les individus ayant eu une mutation avantageuse pour une modification de l’environnement survivent et ont une descendance alors que ceux ayant une mutation désavantageuse pour cette modification environnementale meurent. L’environnement ne déclenche donc pas les mutations. »

Je leur demande également de revenir sur le degré de confiance établi en début de séance. Comme la majorité avait fortement confiance en l’hypothèse de SAINT-HILAIRE, certains élèves prennent conscience qu’ils étaient trop certains d’eux et qu’il aurait fallu être plus prudent.

Lors de la séance suivante, je fais un retour sur les notions et je prends un peu de temps pour discuter des limites de la simulation et évoquer les relations entre Wallace et Darwin.

IV. En guise de conclusion

Comme les autres séances de programmation avec Scratch, cette séance est intéressante à réaliser avec les élèves. Les élèves ont maintenant l’habitude et sont plus autonomes et plus rapides. Ils s’entraident et terminent rapidement la séance. C’est pourquoi j’ai pris le temps de travailler sur le degré de confiance envers une hypothèse.

En cliquant ici, vous pouvez retrouver le programme scratch complet (L’hypothèse de Wallace est par défaut. Modifier le script pour voir l’hypothèse de Saint-Hilaire.)

La fiche tutoriel fournie aux élèves :

Un exemple de fiche activité fournie aux élèves :