Interpoler pour modéliser la topographie du fond des océans
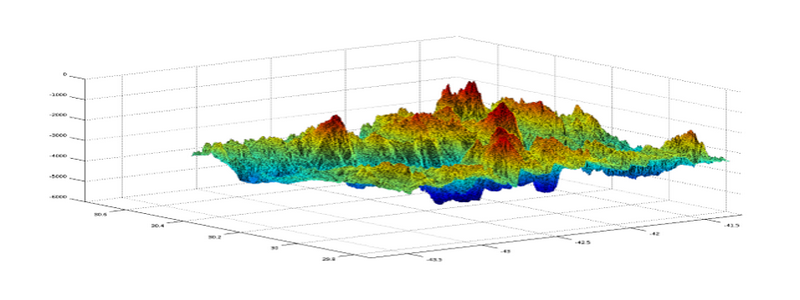
Les données obtenues lors d’une expérience ou lors d’une campagne de prospection sont en général réparties sur une grille irrégulière.
Or les logiciels comme Excel, Scilab, Octave ou Mathlab ne peuvent modéliser une surface qu’à partir d’une grille régulière.
Nous devons donc utiliser des outils d’interpolation pour pallier ce problème... mais qu’est-ce que l’interpolation implique-t-elle dans le traitement des données ?
1/ Le projet
Mesurer la topographie des fonds océaniques a notamment été l’objet d’un sujet de TPE (Travaux Personnels Encadrés) en classe de 1ère S.
Le niveau en mathématique des élèves devant être suffisamment avancé, il semble compliqué d’aborder ce sujet en Collège. De plus, la présence d’un collègue de Mathématiques, Nicolas Krzewina (Lycée Guillaume Apollinaire, à Thiais), a été très profitable, voire indispensable.
L’objectif premier est d’expliquer comment on peut déterminer la topographie du fond des océans, dans des zones pourtant le plus souvent jamais atteintes par l’Homme. Mais d’autres objectifs suivent comme : élaborer un modèle scientifique, utiliser un tableur ou un autre logiciel afin de représenter une surface... et dans ce dernier cas, il faut procéder à des interpolations.
Pour mieux comprendre l’intérêt des interpolations (pour davantage de détails, voir le 3/ Interpoler : pour quoi faire ?), il est très utile de réaliser une maquette représentant le bateau de prospection, les faisceaux issus du sondeur ainsi que différents types de fonds.
Il est également nécessaire de récupérer des données réelles.
2/ L’origine des données
Les données ont 2 origines :
- les résultats issus de l’utilisation de la maquette ;
- les résultats d’une campagne de relevés bathymétriques fournis par Javier Escartin, directeur de recherches au CNRS (Centre National de la Recherche Scientifique) et chercheur à l’IPGP (Institut de Physique du Globe de Paris) sous la forme d’un fichier en .xyz (qui correspond à une matrice), particulièrement volumineux, d’une taille supérieure à 400 Mo, mais néanmoins téléchargeable.
L’IFREMER (Institut Français de Recherche pour l’Exploitation de la MER) a mis à disposition un certain nombre de données sur son site internet :
Au moment du projet réalisé, nous n’avons pu accéder à des données de bathymétrie, mais depuis, la banque de données s’enrichit régulièrement et pourrait constituer une source de données à l’avenir.
3/ Interpoler : pour quoi faire ?
On pourrait naïvement penser qu’il suffit d’avoir des données pour représenter les surfaces souhaitées dans un second temps... mais ce n’est pas si simple : Comment relier les points entre eux ?
De plus, en pratique, les points ne seront jamais parfaitement alignés comme sur un damier (qui est un exemple de matrice régulière) : ils forment alors une matrice irrégulière.
Or les logiciels de représentation graphique des surfaces ont besoin de disposer d’une matrice régulière.
Il existe donc une étape centrale et indispensable de traitement des données : l’interpolation, qui permet de passer d’une matrice irrégulière à une matrice régulière.
Avez-vous déjà utilisé Excel ou un autre tableur équivalent pour construire des graphiques ?
Vous n’aurez aucun problème si toutes vos cases du tableau de données sont remplies. Sinon, le logiciel, par défaut, attribuera une valeur de 0 aux cases vides. Si certaines manipulations (par exemple via une programmation interne au logiciel) sont possibles pour éviter ce mécanisme avec des graphiques en 2 dimensions, ce n’est pas possible avec des graphiques en 3 dimensions.
Il est donc indispensable de combler ces cases vides avec des valeurs estimés par l’expérimentateur qui intervient donc dans la réalisation du graphique.
On ne peut pas fabriquer, directement à partir de données, un graphique représentant une surface en 3D.
Si l’on veut éviter d’attribuer arbitrairement une valeur à ces cases vides, il est donc indispensable d’interpoler.
Voici quelques logiciels permettent d’interpoler :
- Matlab
- Octave
- Scilab
Nous avons, dans le cadre de notre projet, utilisé Octave, logiciel qui nous a permis d’obtenir l’image ci-dessous, à partir du fichier téléchargeable fourni par l’IPGP :
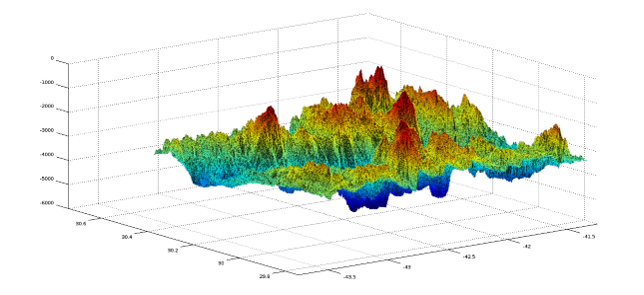
Pour mieux comprendre l’interpolation, prenons quelques exemples extraits de « Utilisation de méthodes d’interpolation pour la régulation de données d’observation. Éléments méthodologiques. » de J-P Labat [1].
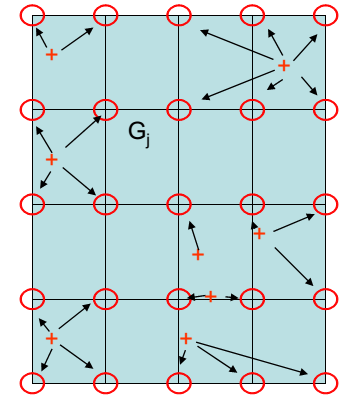
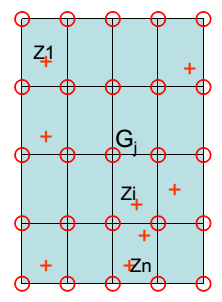
Nous avons ici 8 points. Il faut construire la grille en déterminant le maillage souhaité. Ensuite, il faut donner à chaque nœud une valeur calculée à partir du nuage de points : c’est l’interpolation.
Dans nos essais à l’aide du logiciel octave, nous avons testé trois types d’interpolations :
- Méthode du plus proche voisin
Chaque nœud de la grille prend la valeur du point le plus proche observé dans le plan (O ; I ; J).
- Méthode d’interpolation linéaire
Z1, Z2, … , Zn sont les profondeurs associées à chaque triplets (xi ; yi ; zi) de notre nuage de points.
On note Gj la valeur du nœud j.
Un coefficient compris entre 0 et 1 noté wij est attribué par le système de programmation aux valeurs zi. La somme de ces coefficients est égale à 1.
On calcule Gj comme combinaison linéaire de z1 ; z2 ; … ; zn de la manière suivante :
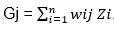
- Méthode de Shepard
La méthode Shepard se base sur la méthode de pondération des plus proches voisins avec pondération par l’inverse de la distance au carrée.
Ici nous avons avec la méthode de l’inverse de la distance :
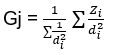
La méthode Shepard introduit un paramètre δ qui permettra un lissage ; Dans cette méthode, nous aurons :
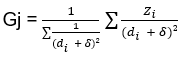
L’interpolation est une étape indispensable, il en existe plusieurs types... mais existe-t-il une interpolation meilleure que les autres ?
4/ Résultats obtenus et choix de l’interpolation
Voici quelques-uns des résultats obtenus grâce aux mesures effectuées avec la maquette :
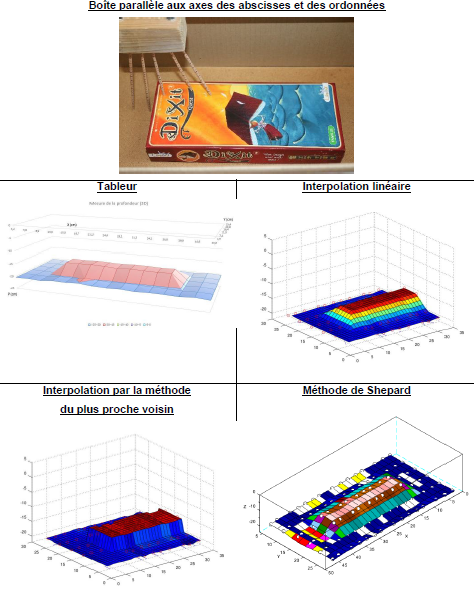
Dans le cas d’un objet en forme de parallélépipède, c’est l’interpolation par la méthode du plus proche voisin qui permet d’obtenir graphiquement les bords les plus proches des bords verticaux de la boite.
Cette méthode d’interpolation est-elle la meilleure ?

Dans le cas d’un objet en forme de demi-sphère, l’interpolation par la méthode du plus proche voisin ne permet d’obtenir que des résultats plus mauvais que les interpolations linéaires et de Shepard.
Existe-t-il une méthode d’interpolation meilleure que d’autres ?
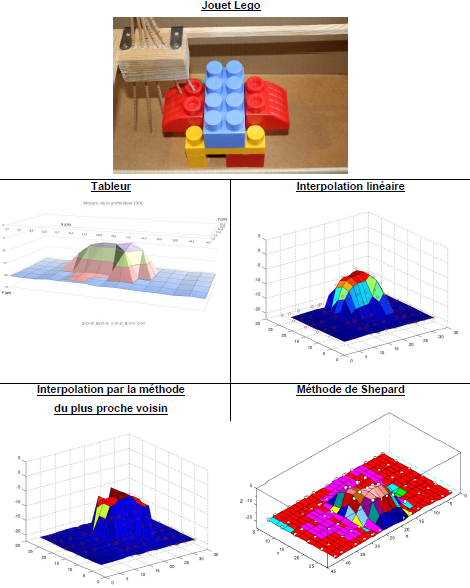
Dans le cas d’un objet avec une forme complexe, construire avec des éléments d’un jeu de construction, aucune méthode d’interpolation ne permet d’obtenir une représentation graphique proche de l’objet. On y retrouve toujours les problèmes liés à une basse définition de l’image, aux points inaccessibles aux faisceaux du sondeur (sous les corniches, dans les grottes et tunnels...).
Il faut garder à l’esprit qu’il n’y a pas de formule magique :
- non seulement il n’existe pas une interpolation qui soit systématique ment meilleure qu’une autre,
- mais dans tous les cas, l’image obtenue est le résultats de traitements mathématiques présentant des approximations...
... donc l’image ou représentation graphique obtenue n’est jamais conforme à 100 % à la réalité.
5/ Conclusion
- Le travail sur l’interpolation permet d’aborder la construction des images scientifiques numériques et de déconstruire le mythe du "plus c’est numérique, plus c’est moderne, meilleur ce sera".
Il n’existe aucune image ou représentation graphique obtenue conforme à 100 % à la réalité : l’être humain intervient dans le choix des interpolations et les interpolations elles-mêmes correspondent à des approximations mathématiques.
- Comment le scientifique fait-il pour choisir l’interpolation la plus efficace dans la situation dans laquelle il se trouve, sachant qu’il n’a pas d’accès direct aux fonds océaniques étudiés ? (contrairement au cas de la maquette qui possédait cet avantage d’accès aux objets réels et d’effectuer le feedback présenté précédemment)
Les scientifiques se basent sur la cohérence entre les images obtenues et la réalité connue : c’est-à-dire qu’ils comparent les images obtenues avec les différentes interpolations avec la réalité connue à d’autres endroits... réalité connue qui correspond donc à leurs connaissances.
Un bon scientifique n’est donc pas seulement un bon technicien ou mathématicien, c’est aussi un "savant".
Cela me semble important pour des élèves (et pas seulement les élèves) que l’apprentissage des connaissances reste primordial : il est indispensable d’avoir des connaissances afin de pouvoir déterminer les informations les plus pertinentes, acte de plus en plus compliqué dans un monde où l’on a accès à des masses d’informations de plus en plus volumineuses.
[1] LABAT J-PH., « Utilisation de méthodes d’interpolation pour la régulation de données d’observation. Éléments méthodologiques. », Analyses de séries long terme, Talence, juin 2012







